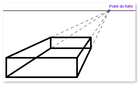
1. Perspective à un point de fuite: construction d'un prisme en 2D

Note: en tout temps, vous pouvez cliquer sur les images pour les agrandir.
Comment faire une perspective à un point de fuite?
En mathématique, une projection est une transformation de l’espace. Elle permet de représenter en deux dimensions un objet à trois dimensions. Il existe plusieurs types de projections.

Dans une projection centrale, certaines arêtes de l’objet qui sont parallèles dans la réalité ne sont pas représentées par des arêtes parallèles.

Il y a plusieurs types de projections centrales, dont la perspective à un point de fuite.

Voyons comment construire un polygone avec Geogebra.
ZONE VIDÉO
Capsule vidéo: 
Comment faire une perspective à un point de fuite?
Défis
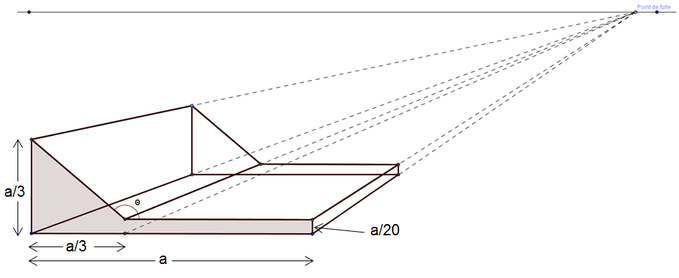
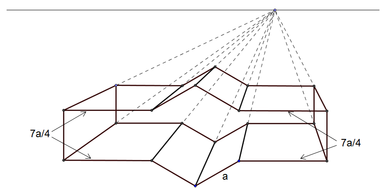
Défi 1: Le plan incliné
Vous voulez construire un plan incliné afin de faire des expériences en physique sur le mouvement d'objets.

Utilisez Geogebra pour obtenir une vue en perspective du plan suivant.
  • sur votre construction, faire afficher la mesure de l'angle;
  • calculer la mesure de l'angle avec l'aide d'un exemple.

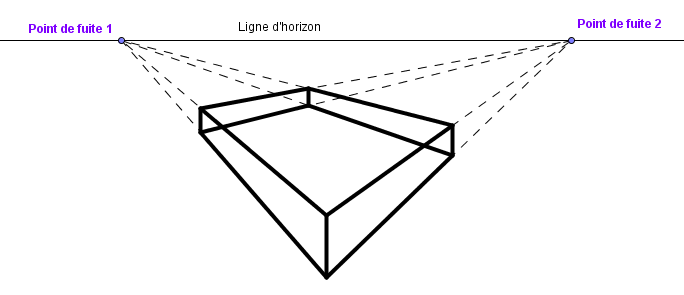
Défi 2: Une perspective à deux points de fuite
Construire, avec Geogebra,  la perspective à deux points de fuite telle qu'illustrée sur l'image suivante.
Défi 3: La clé hexagonale (degré de difficulté plus élevé)
Un entrepreneur qui fabrique des jouets pour enfants désire ajouter une clé hexagonal au coffre d'outils en plastique offert dans son catalogue.

Utilisez Geogebra pour obtenir la construction de la clé hexagonale suivante. 
  • cette clé est munie d'un hexagone régulier en son centre, dont les côtés mesurent "a";
  • les 4 segments situés à l'avant-plan mesurent chacun 7a/4 et sont parallèles deux à deux.