3. Le nuage de points
Note: en tout temps, vous pouvez cliquer sur les images pour les agrandir.
Introduction
Les cours de modélisation algébrique et graphique, en commençant par le cours MAT-3051, abordent la notion de nuage de points. On doit amener les élèves à trouver le modèle algébrique théorique qui représente le plus fidèlement possible un nuage quelconque de points.
|
Comment trouver un modèle représentatif d'un nuage de points avec Geogebra?
|
|
Avec Geogebra, nous pouvons utiliser des "Commandes" qui permettent de créer des nouveaux objets ou de modifier des objets existants. On peut accéder à ces commandes de plusieurs façon.
En débutant l'écriture du mot "Med" par exemple, une série de commande apparaissent parmi lesquelles je peux choisir...
|
Une liste complète de commandes apparaissent lorsque l'on clique sur l'aide saisie.
|
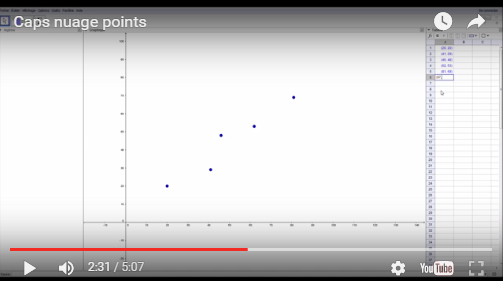
À partir d'un nuage de points, il est possible d'utiliser la commande "Ajustement" qui permet de tracer une droite ou une courbe qui modélise algébriquement ce nuage.
ZONE VIDÉO
|
Capsule vidéo:
Comment trouver un modèle algébrique représentatif d'un nuage de points avec Geogebra? |
|
|
Défi 1: La consommation d'essence
|
|
Cette situation-problème peut s'appliquer dans le cadre du cours MAT-3051 Modélisation algébrique et graphique. Tentez de la résoudre avec Geogebra.
Mise en situation
Deux couples d'amis partent en voyage avec leurs enfants. Ils font le plein de chacune des deux voitures avant de partir.
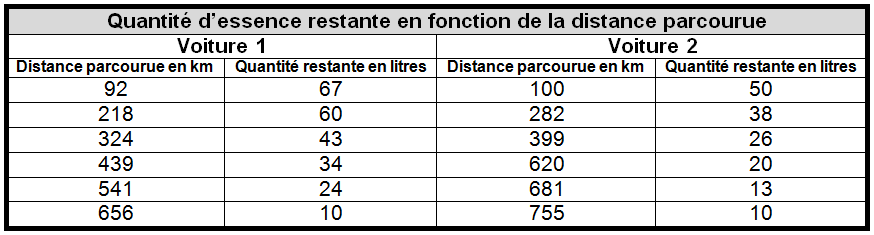
Voici des tableaux illustrant la quantité d'essence restante de chacune des voitures en fonction de la distance parcourue.
Deux couples d'amis partent en voyage avec leurs enfants. Ils font le plein de chacune des deux voitures avant de partir.
Voici des tableaux illustrant la quantité d'essence restante de chacune des voitures en fonction de la distance parcourue.
| consommation_essence.docx |
Questions
Répondre aux questions suivantes en traitant la situation avec Geogebra.
1. Sur les fiches techniques des voitures, la consommation d'essence est indiquée en L/100 km. Trouver cette valeur pour chacune des voitures.
2. Pouvez-vous estimer la quantité d'essence que représente un plein pour chacune des voitures?
3. La destination se trouve à 850 km du point de départ. Les voitures auront-elles suffisamment d'essence pour se rendre à destination sans arrêter pour en reprendre?
Répondre aux questions suivantes en traitant la situation avec Geogebra.
1. Sur les fiches techniques des voitures, la consommation d'essence est indiquée en L/100 km. Trouver cette valeur pour chacune des voitures.
2. Pouvez-vous estimer la quantité d'essence que représente un plein pour chacune des voitures?
3. La destination se trouve à 850 km du point de départ. Les voitures auront-elles suffisamment d'essence pour se rendre à destination sans arrêter pour en reprendre?
|
Défi 2: On se rejoint?
|
|
Cette situation-problème peut s'appliquer dans le cadre du cours MAT-3051 Modélisation algébrique et graphique. Tentez de la résoudre avec Geogebra.
Mise en situation
Deux voitures partent du même point. Une première voiture démarre et quelques minutes plus tard, la deuxième démarre à son tour en roulant un peu plus rapidement que la première. Les deux voitures roulent par la suite à vitesse constante.
Est-il possible de déterminer le moment où les deux voitures se rejoindront?
|
Deux robots qui se suivent…
Dans l’expérience qui suit, remplaçons les voitures de la mise en situation par deux robots qui partent d’un même point, mais à des temps différents. Visionnez la vidéo. |
|
Questions
Répondre aux questions suivantes en traitant la situation avec Geogebra.
1. Les deux robots se rejoindront-ils? Et si c’est le cas, trouvez à quel moment ils se rejoindront et quelle distance aura parcourue chacun des robots?
2. Quelle distance séparera les deux robots après 5 minutes?
3. Trouvez la vitesse de chacun des robots.
Répondre aux questions suivantes en traitant la situation avec Geogebra.
1. Les deux robots se rejoindront-ils? Et si c’est le cas, trouvez à quel moment ils se rejoindront et quelle distance aura parcourue chacun des robots?
2. Quelle distance séparera les deux robots après 5 minutes?
3. Trouvez la vitesse de chacun des robots.
|
Défi 3: Un voyage à Sherbrooke
|
|
Cette situation-problème peut s'appliquer dans le cadre du cours MAT-3051 Modélisation algébrique et graphique. Tentez de la résoudre avec Geogebra.
Mise en situation
Vous et quelques amis vous rendez pour une fin de semaine à Sherbrooke afin de participer à une fête chez un autre ami du groupe. Vous prenez deux voitures puisque vous êtes nombreux et ne partez pas tous du même endroit.
En voiture
Une première voiture part de Gatineau, et une deuxième, de Buckingham. Les voitures partent en même temps, soit à 18 heures, et empruntent les mêmes routes.
Mise en situation
Vous et quelques amis vous rendez pour une fin de semaine à Sherbrooke afin de participer à une fête chez un autre ami du groupe. Vous prenez deux voitures puisque vous êtes nombreux et ne partez pas tous du même endroit.
En voiture
Une première voiture part de Gatineau, et une deuxième, de Buckingham. Les voitures partent en même temps, soit à 18 heures, et empruntent les mêmes routes.
La voiture 1, partant de Buckingham, se déplace selon les informations du tableau suivant :
La voiture 2, partant de Gatineau, s’arrête à une station-service à 19 h 35 après avoir parcouru 170 km. Après une halte de 5 minutes, elle repart et arrive à Sherbrooke à 21 h 25.
Questions
Répondre aux questions suivantes en traitant la situation avec Geogebra.
1. Les deux voitures se rejoignent-elles à un moment donné du trajet? Si oui, à quel moment?
2. Dans la dernière portion du trajet, après les haltes, à quelle vitesse la voiture la plus lente de cette portion devrait-elle rouler pour arriver à destination en même temps que l’autre?
3. Quelle distance sépare les deux voitures après 75 minutes de route?
Répondre aux questions suivantes en traitant la situation avec Geogebra.
1. Les deux voitures se rejoignent-elles à un moment donné du trajet? Si oui, à quel moment?
2. Dans la dernière portion du trajet, après les haltes, à quelle vitesse la voiture la plus lente de cette portion devrait-elle rouler pour arriver à destination en même temps que l’autre?
3. Quelle distance sépare les deux voitures après 75 minutes de route?
